Постоянство и крекеры
29.05.2008 в 17:23
Пишет Trotil:Виды магических квадратов.
Самый известный магический квадрат:
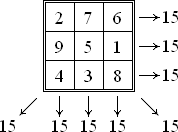
Оказывается, существует целая классификация магических квадратов. Итак:
Магический квадрат — это квадратная таблица n x n, заполненная n2 числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.
Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой МК, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата (картинка разломанных диагоналей).
Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.
По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.
Также опубликовано здесь
URL записиСамый известный магический квадрат:

Оказывается, существует целая классификация магических квадратов. Итак:
Магический квадрат — это квадратная таблица n x n, заполненная n2 числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.
Нормальный МК - магический квадрат, заполненный целыми числами от 1 до n2.
Полумагический квадрат - квадрат, заполненный числами от 1 до n2., называется полумагическим, если сумма чисел по горизонталям и вертикалям равна магической постоянной, а по диагоналям это условие не выполняется.
Aссоциативный, или симметричный МК, такой МК, у которого сумма любых двух чисел, симметрично расположенных относительно центра квадрата, равна одному и тому же числу: 1+n2.
Пандиагональный (дьявольский) МК - такой магический квадрат, в котором сумма чисел по разломанным диагоналям также равна константе квадрата (картинка разломанных диагоналей).
Идеальный МК - магический квадрат, который одновременно пандиагональный и ассоциативный.
Совершенный МК - магический пандиагональный квадрат порядка 4k, обладающий дополнительными свойствами.
Бимагический квадрат - такой магический квадрат, который остаётся магическим при замене всех его элементов на их квадраты. Бимагических квадратов 3,4,5 порядка не существует.
Мультимагический квадарат - обобщение бимагических квадратов на произвольную степень n.
По этой ссылке можно узнать количестве разных видов МК. Но там не учитываются изоморфные преобразования МК (когда один МК переходит в другой поворотом, сдвигом и т.д.) При подсчете они считались различными.
Также опубликовано здесь